Priority Queue Implementation in Rust

This article will describe a more complex data structure called Priority Queue. We will implement it with a Binary Heap, a data structure that takes the form of a tree.

Usage

In general, Priority Queue supports these operations:

Insert an element to the queue in an O(log N) time.
Pop the maximum element from the queue in O(log N) time. (or minimum, depends on the implementation)
Get the length of the queue.

This data structure is quite helpful in many applications. For example, the OS kernel can order CPU tasks by priority or, maybe, required execution time.

Idea behind Binary Heap

As mentioned earlier, we can implement Binary Heap to support the operations of Priority Queue.

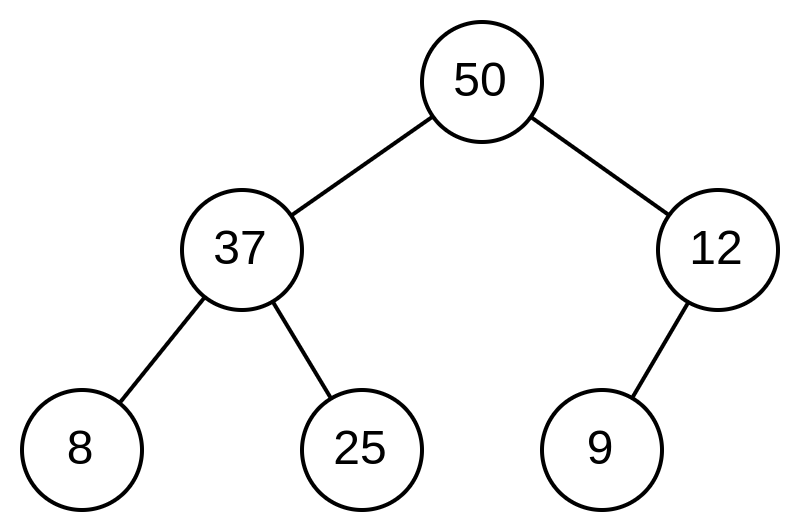
The Max Binary Heap is a tree data structure that holds these properties:

The key stored in each node is greater and equal to the keys in the node's children.
This data structure is a complete binary tree. All levels of the tree are filled, except the last one, which can have missing nodes on the right.

Priority Queue

Binary Heap Implementation

We can implement this data structure without pointers at all. The idea is that a complete binary tree can be implemented as a Vector. For example: vec[0] can be the root, it’s left and right children are vec[1] and vec[2], their children are vec[3], vec[4] and vec[5], vec[6].

Let’s start with this basic code:

#[derive(Default, Debug)]
pub struct BinaryHeap<T> {
    nodes: Vec<T>,
}

impl<T> BinaryHeap<T>
where
    T: Ord,
{
    pub fn new() -> Self {
        Self { nodes: Vec::new() }
    }

    pub fn with_capacity(capacity: usize) -> Self {
        Self {
            nodes: Vec::with_capacity(capacity),
        }
    }

    pub fn len(&self) -> usize {
        self.nodes.len()
    }

    pub fn is_empty(&self) -> bool {
        self.len() == 0
    }

    fn parent(idx: usize) -> usize {
        (idx - 1) / 2
    }

    fn left_child(idx: usize) -> usize {
        idx * 2
    }

    fn right_child(idx: usize) -> usize {
        idx * 2 + 1
    }
}

impl<T> Clone for BinaryHeap<T>
where
    T: Clone,
{
    fn clone(&self) -> Self {
        Self {
            nodes: self.nodes.clone(),
        }
    }
}

BinaryHeap structure contains the vector of nodes to represent a complete binary tree. It already implements Default, Debug and Clone traits. I also added common methods len, is_empty, new, and with_capacity.

Methods parent, left_child, and right_child are here to index inside the array.

Push method

To insert an element, we should add it to the end of the array, and until the properties of Binary Heap are held, we will move the element up.

pub fn push(&mut self, item: T) {
    self.nodes.push(item);
    self.lift_up(self.nodes.len() - 1);
}

fn lift_up(&mut self, idx: usize) {
    if idx == 0 {
        return;
    }

    let parent = Self::parent(idx);
    if self.nodes[parent].cmp(&self.nodes[idx]).is_le() {
        self.nodes.swap(parent, idx);
        self.lift_up(parent);
    }
}

Pop method

Remember, we are popping the maximum element from the tree’s root. It means we should delete the first element and rebuild the tree to hold the Binary Heap properties.

The code is following:

pub fn pop(&mut self) -> Option<T> {
    if self.nodes.is_empty() {
        None
    } else {
        let last_idx = self.len() - 1;
        self.nodes.swap(0, last_idx);
        self.lift_down(0, last_idx);

        self.nodes.pop()
    }
}

fn lift_down(&mut self, idx: usize, len: usize) {
    let left_child = Self::left_child(idx);
    let right_child = Self::right_child(idx);

    let mut biggest = idx;
    if left_child < len && self.nodes[biggest].cmp(&self.nodes[left_child]).is_le() {
        biggest = left_child;
    }

    if right_child < len && self.nodes[biggest].cmp(&self.nodes[right_child]).is_le() {
        biggest = right_child;
    }

    if biggest != idx {
        self.nodes.swap(idx, biggest);
        self.lift_down(biggest, len);
    }
}

Conversion to a sorted vector

One helpful method is to convert the Priority Queue to the sorted vector. To do that, we need to do the same operation as during the pop. Here is the code:

pub fn into_sorted_vec(mut self) -> Vec<T> {
    let len = self.len();

    for i in (1..len).rev() {
        self.nodes.swap(0, i);
        self.lift_down(0, i);
    }

    self.nodes
}

Final Code

To verify our implementation, I added the tests. You can review the final code in my public repo.

Usage#

Idea behind Binary Heap#

Binary Heap Implementation#

Push method#

Pop method#

Conversion to a sorted vector#

Final Code#