This article describes an advanced data structure called Segment Tree and provides implementation in the popular modern language Golang. We will solve a problem in SPOJ to show how we can use the Segment Tree in competitive programming.
General Idea
Segment Tree is an advanced tree data structure that allows you to answer range queries efficiently and modify the array quickly. Segment Tree is commonly used in competitive programming to solve problems in O(n log n) time. That includes finding the sum of consecutive array elements, minimum or maximum in the range, maximum consecutive range sum, etc. This structure is more flexible than Fenwick Tree and allows you to solve more complex problems but is more challenging in implementation.
Segment Tree Structure
Let’s review the simplest problem that can be solved with the Segment tree. You are given an array arr, and you should handle two types of queries:
- find the sum of the array elements between the indices
landr; - modify an element of the array.
You should process these queries in O(log n) time. Segment Tree can solve such a problem much more efficiently than brute force solution, which will update the element in O(1) time but find the sum in O(n) time.
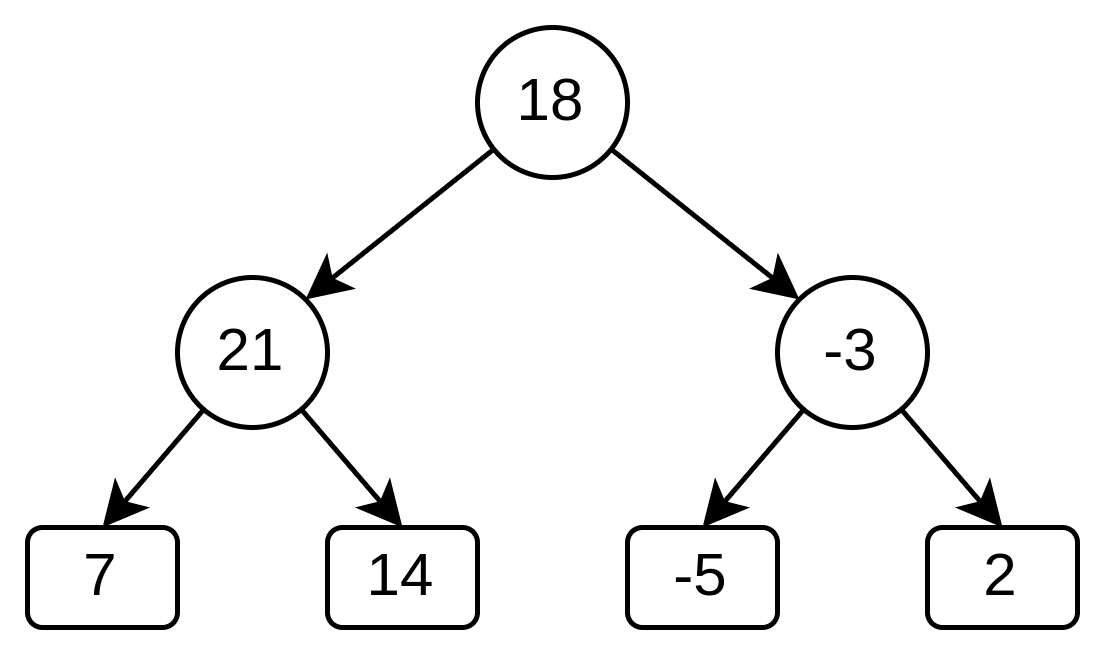
Let’s imagine we have an array [7, 14, -5, 2]. The root node will contain the sum of the whole array, 18. Its left child will have the sum of the first two elements 7+14=21, and the right child will be -5+2=-3. You can see an example Segment Tree for this problem below.
To represent such a tree in your program, we can use a single-dimensional array with length 4n, where n is the array’s length. We can use this formula to express the dependency between parents and children. Let the parent node be a node with index i inside the array. His left child will be a node with index i*2, and right child will be a node with index i*2+1. With such a formula, we will utilize almost all cells inside the array and benefit from memory proximity. The example is presented below.
Golang implementation
Problem description
In this section, we will solve a more complex problem from the popular online problem catalog SPOJ using popular modern language Golang. You can find the problem here (link).
Data structure definition
We should store a more complex data structure inside the Segment Tree node to find the maximum range sum. The idea is to store prefix, suffix, total sum, and best range sum for each node:
type SegmentTreeData struct {
prefix int
suffix int
best int
total int
}
Let’s review the node with length 1. All the properties will be the same because the best prefix of the array with length 1 equals the suffix, total sum and it’s the best range sum.
func createData(value int) SegmentTreeData {
return SegmentTreeData{
prefix: value,
suffix: value,
best: value,
total: value,
}
}
The algorithm becomes more interesting with bigger segments. We can merge two nodes by using this algorithm:
prefix = max(left.prefix, left.totalSum + right.prefix);suffix = max(right.suffix, right.totalSum + left.suffix);totalSum = left.totalSum + right.totalSum;best = max(left.best, right.best, prefix, suffix, left.suffix + right.prefix);
func merge(left, right SegmentTreeData) SegmentTreeData {
total := left.total + right.total
prefix := max(left.prefix, left.total+right.prefix)
suffix := max(right.suffix, right.total+left.suffix)
best := max(
left.best,
right.best,
prefix,
suffix,
left.suffix+right.prefix,
)
return SegmentTreeData{
prefix,
suffix,
best,
total,
}
}
Segment Tree data structure should consist of n * 4 nodes, where n is the array’s length.
type SegmentTree struct {
n int
data []SegmentTreeData
}
Build initial data structure
To build an initial data structure, we should recursively dive deep from the top of the tree to the bottom. A leaf node can be easily constructed by using createData defined before. Otherwise, we should build left and right nodes and then merge their data structures using the merge method. This algorithm will run in O(n) time because the length of the tree is 4 * n.
func Build(arr []int) *SegmentTree {
n := len(arr)
length := n * 4
data := make([]SegmentTreeData, length)
tree := &SegmentTree{
n,
data,
}
tree.build(arr, 1, 1, n)
return tree
}
func (tree *SegmentTree) build(arr []int, index int, left int, right int) {
if left > right {
return
} else if left == right {
tree.data[index] = createData(arr[left-1])
} else {
middle := (left + right) / 2
tree.build(arr, index*2, left, middle)
tree.build(arr, index*2+1, middle+1, right)
tree.data[index] = merge(tree.data[index*2], tree.data[index*2+1])
}
}
Update single element
The update operation is not much different from the build and runs in O(log n) time. Firstly, we should find and update the element with the new value. Secondly, we should go up and update all the nodes that were impacted. To update the node, we should, as before, merge its left and right children.
func (tree *SegmentTree) Update(x, y int) {
tree.update(1, 1, tree.n, x, y)
}
func (tree *SegmentTree) update(index int, left int, right int, updateIndex int, updateValue int) {
if left > right || left > updateIndex || right < updateIndex {
return
} else if left == right {
tree.data[index] = createData(updateValue)
} else {
middle := (left + right) / 2
tree.update(index*2, left, middle, updateIndex, updateValue)
tree.update(index*2+1, middle+1, right, updateIndex, updateValue)
tree.data[index] = merge(tree.data[index*2], tree.data[index*2+1])
}
}
Find max range sum
Finally, we should answer queries in O(log n) time using our tree data structure. Once again, we have 3 cases here:
- The requested range matches to
noderange. We can return its internal data. - The requested range is smaller than the
node’s and lies in one of its children. We can recursively call the function inside that children. - The requested range is smaller than the
node’s and occupies both children. We should recursively build answers for both of them and merge the result using the merge function.
func (tree *SegmentTree) Find(x, y int) int {
return tree.find(1, 1, tree.n, x, y).best
}
func (tree *SegmentTree) find(index int, left int, right int, findLeft int, findRight int) SegmentTreeData {
if left == findLeft && right == findRight {
return tree.data[index]
} else {
middle := (left + right) / 2
if findRight <= middle {
return tree.find(index*2, left, middle, findLeft, findRight)
} else if findLeft > middle {
return tree.find(index*2+1, middle+1, right, findLeft, findRight)
} else {
leftResult := tree.find(index*2, left, middle, findLeft, min(middle, findRight))
rightResult := tree.find(index*2+1, middle+1, right, max(findLeft, middle+1), findRight)
mergedResult := merge(leftResult, rightResult)
return mergedResult
}
}
}
IO processing
To solve the competitive programming problem, we should read the input from stdin and output the result to stdout. Golang lacks clean console io support. That’s why we should write some boilerplate code by ourselves. First, we should use buffers to read from stdin and write to stdout. Secondly, to read the entire array, we should read the whole line as a string, trim it, and split it by spaces. Then we should convert this string array to an int array. The single number read and write can be done using the fmt package.
var reader *bufio.Reader = bufio.NewReader(os.Stdin)
var writer *bufio.Writer = bufio.NewWriter(os.Stdout)
func readInt() int {
var value int
fmt.Fscanf(reader, "%d\n", &value)
return value
}
func writeInt(value int) {
fmt.Fprintln(writer, value)
}
func readArray(n int) []int {
line, err := reader.ReadString('\n')
if err != nil {
panic(err)
}
stringArray := strings.Split(strings.TrimSpace(line), " ")
if len(stringArray) != n {
panic(fmt.Errorf("Expected input array to be of size %d, but was %d", n, len(stringArray)))
}
arr := make([]int, n)
for i := 0; i < n; i++ {
value, err := strconv.Atoi(stringArray[i])
if err != nil {
panic(err)
}
arr[i] = value
}
return arr
}
Main function
The latest part is the main function. First, we should flush our buffers to output the result correctly. Then we can read the input array and build the Segment Tree data structure using the Build function defined before.
To process each query, we can use either tree.Update or tree.Find function. The result of find operation should be written to the stdout.
func main() {
defer writer.Flush()
n := readInt()
arr := readArray(n)
tree := Build(arr)
m := readInt()
for i := 0; i < m; i++ {
query := readArray(3)
t := query[0]
x := query[1]
y := query[2]
if t == 0 {
tree.Update(x, y)
} else {
value := tree.Find(x, y)
writeInt(value)
}
}
}
Final code
You can now submit your solution to the SPOJ website and verify the result. The system should accept it unless you missed some parts in your implementation. My solution took 0.09 seconds and 14M memory. That’s enough to be considered successful. The time limit for this problem is 1 second and 1536M memory.
package main
import (
"bufio"
"fmt"
"os"
"strconv"
"strings"
)
type SegmentTreeData struct {
prefix int
suffix int
best int
total int
}
func createData(value int) SegmentTreeData {
return SegmentTreeData{
prefix: value,
suffix: value,
best: value,
total: value,
}
}
func merge(left, right SegmentTreeData) SegmentTreeData {
total := left.total + right.total
prefix := max(left.prefix, left.total+right.prefix)
suffix := max(right.suffix, right.total+left.suffix)
best := max(
left.best,
right.best,
prefix,
suffix,
left.suffix+right.prefix,
)
return SegmentTreeData{
prefix,
suffix,
best,
total,
}
}
type SegmentTree struct {
n int
data []SegmentTreeData
}
func Build(arr []int) *SegmentTree {
n := len(arr)
length := n * 4
data := make([]SegmentTreeData, length)
tree := &SegmentTree{
n,
data,
}
tree.build(arr, 1, 1, n)
return tree
}
func (tree *SegmentTree) build(arr []int, index int, left int, right int) {
if left > right {
return
} else if left == right {
tree.data[index] = createData(arr[left-1])
} else {
middle := (left + right) / 2
tree.build(arr, index*2, left, middle)
tree.build(arr, index*2+1, middle+1, right)
tree.data[index] = merge(tree.data[index*2], tree.data[index*2+1])
}
}
func (tree *SegmentTree) Update(x, y int) {
tree.update(1, 1, tree.n, x, y)
}
func (tree *SegmentTree) update(index int, left int, right int, updateIndex int, updateValue int) {
if left > right || left > updateIndex || right < updateIndex {
return
} else if left == right {
tree.data[index] = createData(updateValue)
} else {
middle := (left + right) / 2
tree.update(index*2, left, middle, updateIndex, updateValue)
tree.update(index*2+1, middle+1, right, updateIndex, updateValue)
tree.data[index] = merge(tree.data[index*2], tree.data[index*2+1])
}
}
func (tree *SegmentTree) Find(x, y int) int {
return tree.find(1, 1, tree.n, x, y).best
}
func (tree *SegmentTree) find(index int, left int, right int, findLeft int, findRight int) SegmentTreeData {
if left == findLeft && right == findRight {
return tree.data[index]
} else {
middle := (left + right) / 2
if findRight <= middle {
return tree.find(index*2, left, middle, findLeft, findRight)
} else if findLeft > middle {
return tree.find(index*2+1, middle+1, right, findLeft, findRight)
} else {
leftResult := tree.find(index*2, left, middle, findLeft, min(middle, findRight))
rightResult := tree.find(index*2+1, middle+1, right, max(findLeft, middle+1), findRight)
mergedResult := merge(leftResult, rightResult)
return mergedResult
}
}
}
func max(x int, rest ...int) int {
mx := x
for _, value := range rest {
if mx < value {
mx = value
}
}
return mx
}
func min(x int, rest ...int) int {
mn := x
for _, value := range rest {
if mn > value {
mn = value
}
}
return mn
}
var reader *bufio.Reader = bufio.NewReader(os.Stdin)
var writer *bufio.Writer = bufio.NewWriter(os.Stdout)
func readInt() int {
var value int
fmt.Fscanf(reader, "%d\n", &value)
return value
}
func writeInt(value int) {
fmt.Fprintln(writer, value)
}
func readArray(n int) []int {
line, err := reader.ReadString('\n')
if err != nil {
panic(err)
}
stringArray := strings.Split(strings.TrimSpace(line), " ")
if len(stringArray) != n {
panic(fmt.Errorf("Expected input array to be of size %d, but was %d", n, len(stringArray)))
}
arr := make([]int, n)
for i := 0; i < n; i++ {
value, err := strconv.Atoi(stringArray[i])
if err != nil {
panic(err)
}
arr[i] = value
}
return arr
}
func main() {
defer writer.Flush()
n := readInt()
arr := readArray(n)
tree := Build(arr)
m := readInt()
for i := 0; i < m; i++ {
query := readArray(3)
t := query[0]
x := query[1]
y := query[2]
if t == 0 {
tree.Update(x, y)
} else {
value := tree.Find(x, y)
writeInt(value)
}
}
}