Rust Doubly Linked List Implementation

Doubly Linked List is the next fundamental collection that is useful to understand. It goes further from Singly Linked List by allowing appending elements from both sides, but this comes at the cost of more complex implementation. This article will cover all the details you need to implement this data structure in Rust.

This article is a continuation of a previous one related to Singly Linked List. Have a look at it if you are unfamiliar with Singly Linked List yet: Rust Singly Linked List Implementation.

General Idea

Doubly Linked List (or Linked List) is a dynamically sized data collection that allows adding and popping elements in constant time from the start and end. These properties must implement other data structures like Stack, Queue, and Deque.

Representation

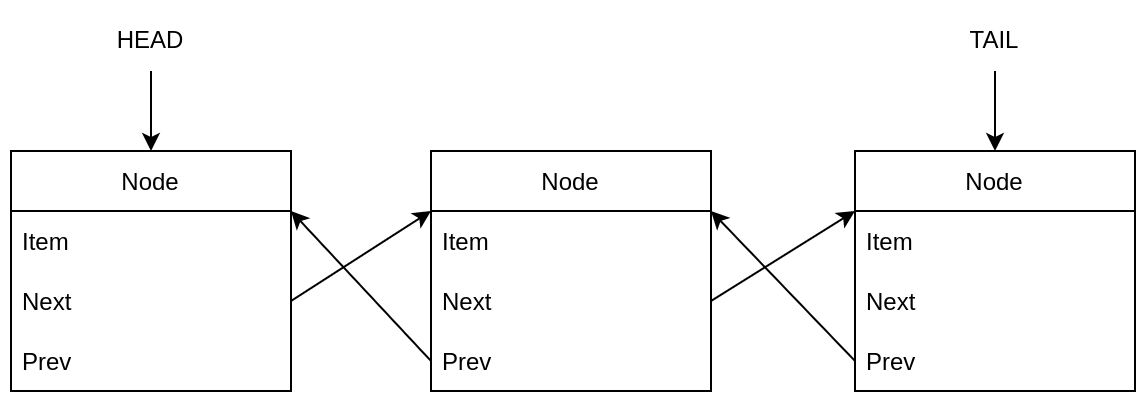
Linked List consists of several Nodes. Each Node contains a value itself and pointers to the Nodes after and before it. There are also two pointers called HEAD and TAIL, pointing to the first Node and the last one, respectively. They are used to push or pop elements from both sides.

Linked List

ListNode Implementation

Let’s start by implementing a ListNode struct.

use std::{cell::RefCell, rc::Rc};

struct ListNode<T> {
    item: T,
    next: Link<T>,
    prev: Link<T>,
}

impl<T> ListNode<T> {
    fn new(item: T) -> Self {
        Self {
            item,
            next: None,
            prev: None,
        }
    }
}

type Link<T> = Option<Rc<RefCell<ListNode<T>>>>;

Firstly, you can see that we added a second link here, compared to Singly Linked List. It’s called prev and is pointing to the previous Node. Note that we are using shorthand type Link<T>, an optional link to the Node. It’s handy to add such types in Rust for convenience.

Doubly Linked List Implementation

Structure and basic methods

Secondly, let’s add the main structure together with the basic methods that are easy to implement:

#[derive(Default)]
pub struct DoublyLinkedList<T> {
    head: Link<T>,
    tail: Link<T>,
    size: usize,
}

impl<T> DoublyLinkedList<T> {
    pub fn new() -> Self {
        Self {
            head: None,
            tail: None,
            size: 0,
        }
    }

    pub fn is_empty(&self) -> bool {
        self.len() == 0
    }

    pub fn len(&self) -> usize {
        self.size
    }
}

We define head and tail, as discussed earlier, to operate on the nodes. Also, we added size variable to implement methods len() and is_empty(), that are useful for collections.

Push methods

Let’s add the push_back method next.

pub fn push_back(&mut self, item: T) {
    let node = Rc::new(RefCell::new(ListNode::new(item)));
    if let Some(prev_tail) = self.tail.take() {
        prev_tail.borrow_mut().next = Some(Rc::clone(&node));
        node.borrow_mut().prev = Some(prev_tail);
        self.tail = Some(node);
        self.size += 1;
    } else {
        self.head = Some(Rc::clone(&node));
        self.tail = Some(node);
        self.size = 1;
    }
}

First of all, we build the new node that should be added. Then we check a case if our list is empty.

If the list is empty, we should point head and tail to the new node and set size to 1.
Otherwise, we assign prev and next pointers appropriately for the tail and newly added node and then point tail to the new location. Size is increased by 1.

The implementation for push_front is similar. We use head instead of tail here.

pub fn push_front(&mut self, item: T) {
    let node = Rc::new(RefCell::new(ListNode::new(item)));
    if let Some(prev_head) = self.head.take() {
        prev_head.borrow_mut().prev = Some(Rc::clone(&node));
        node.borrow_mut().next = Some(prev_head);
        self.head = Some(node);
        self.size += 1;
    } else {
        self.head = Some(Rc::clone(&node));
        self.tail = Some(node);
        self.size = 1;
    }
}

Pop methods

Pop methods are a little more complicated, but I will go line by line to explain them.

pub fn pop_back(&mut self) -> Option<T> {
    self.tail.take().map(|prev_tail| {
        self.size -= 1;
        match prev_tail.borrow_mut().prev.take() {
            Some(node) => {
                node.borrow_mut().next = None;
                self.tail = Some(node);
            }
            None => {
                self.head.take();
            }
        }
        Rc::try_unwrap(prev_tail).ok().unwrap().into_inner().item
    })
}

Remember that tail is Link<T> which is Option<...>? Option has a map method that will apply a function to the Some(...) value or return None otherwise.

That means, if the List is empty, we will return None, and the function will not be called. Otherwise, it will be called, and we will return an item from the tail.

The function implementation is straightforward: if the tail has the previous Node, we will point the tail to it and remove the next pointer. Otherwise, we should empty the head and tail, as the size is 0, and they should be None.

The last line unwraps the Node, moves value out of RefCell by calling into_inner(), and returns .item property. The result of this function is then wrapped in Some(...).

The implementation of pop_front is similar:

pub fn pop_front(&mut self) -> Option<T> {
    self.head.take().map(|prev_head| {
        self.size -= 1;
        match prev_head.borrow_mut().next.take() {
            Some(node) => {
                node.borrow_mut().prev = None;
                self.head = Some(node);
            }
            None => {
                self.tail.take();
            }
        }
        Rc::try_unwrap(prev_head).ok().unwrap().into_inner().item
    })
}

Drop Implementation

As you may have noticed, we are using Rc<RefCell<...>> to refer to the node in our code. Rc is an intelligent pointer in Rust that allows several references to the exact location. The value is stored in a heap and will be removed only when the references count equals 0. The advantage of this pointer is that the borrow checker will not complain about using it, and it’s entirely safe to do so. However, there is one caveat here.

As we have cycle references in our Linked List, the count will never become 0, and the value will be stuck in memory forever! To handle that case, we should implement the Drop trait ourselves and remove references from all the Nodes. Hopefully, the implementation is simple enough:

impl<T> Drop for DoublyLinkedList<T> {
    fn drop(&mut self) {
        while let Some(node) = self.head.take() {
            let _ = node.borrow_mut().prev.take();
            self.head = node.borrow_mut().next.take();
        }
        self.tail.take();
    }
}

This code replaces self.head and self.tail with None and drops their initial values. Then it traverses all the Nodes from head to the tail, replacing their prev and next links.

This removes all the references in the memory, and Rc implementation will drop the values behind the scenes.

To check that this will work, we can create a dumb structure called Token and add it to the ListNode like this:

struct Token {}

impl Token {
    fn new() -> Self {
        println!("CREATED");
        Self {}
    }
}

impl Drop for Token {
    fn drop(&mut self) {
        println!("DESTROYED");
    }
}

struct ListNode<T> {
    item: T,
    next: Link<T>,
    prev: Link<T>,
    token: Token,
}

impl<T> ListNode<T> {
    fn new(item: T) -> Self {
        Self {
            item,
            next: None,
            prev: None,
            token: Token::new(),
        }
    }
}

Then we can write a test like this to verify it:

#[test]
fn it_drops_correctly() {
    let mut list = DoublyLinkedList::new();
    for i in 0..3 {
        list.push_back(i);
    }

    drop(list);
}

And run it:

➜  linkedlist git:(double-linked-list) cargo t it_drops_correctly -- --nocapture
   Compiling linkedlist v0.1.0 (/home/rostyslav/Programming/linkedlist)
    Finished test [unoptimized + debuginfo] target(s) in 0.71s
     Running unittests (target/debug/deps/linkedlist-32e634d8d6bef48f)

running 1 test
CREATED
CREATED
CREATED
DESTROYED
DESTROYED
DESTROYED
test doubly_linked_list::tests::it_drops_correctly ... ok

test result: ok. 1 passed; 0 failed; 0 ignored; 0 measured; 12 filtered out; finished in 0.00s

As you can see, there were 3 items added to the list, and the program removed them all. It works!

Iterator Implementation

To be more user-friendly, we can add the Iterator trait. As our Linked List is double-ended, we can also implement DoubleEndedIterator. Here are implementations:

impl<T> IntoIterator for DoublyLinkedList<T> {
    type Item = <ListIterator<T> as Iterator>::Item;

    type IntoIter = ListIterator<T>;

    fn into_iter(self) -> Self::IntoIter {
        Self::IntoIter::new(self)
    }
}

pub struct ListIterator<T> {
    list: DoublyLinkedList<T>,
}

impl<T> ListIterator<T> {
    fn new(list: DoublyLinkedList<T>) -> Self {
        Self { list }
    }
}

impl<T> Iterator for ListIterator<T> {
    type Item = T;

    fn next(&mut self) -> Option<Self::Item> {
        self.list.pop_front()
    }
}

impl<T> DoubleEndedIterator for ListIterator<T> {
    fn next_back(&mut self) -> Option<Self::Item> {
        self.list.pop_back()
    }
}

I created a separate struct called ListIterator. It can be constructed by implementing the IntoIterator trait for DoublyLinkedList. Then, we can use pop_front and pop_back methods to implement the iterator. Simple enough!

Testing

To verify everything works fine, we should add tests. Here are the tests created by me. Fill free to add more tests and verify more sophisticated cases.

#[cfg(test)]
mod tests {
    use super::DoublyLinkedList;

    #[test]
    fn it_works() {
        let mut list = DoublyLinkedList::new();

        list.push_back(3);
        list.push_back(4);
        assert_eq!(list.pop_front(), Some(3));
        assert_eq!(list.len(), 1);

        list.push_front(5);
        assert_eq!(list.pop_back(), Some(4));
        assert_eq!(list.pop_back(), Some(5));
        assert_eq!(list.pop_back(), None);
        assert_eq!(list.pop_front(), None);
        assert_eq!(list.len(), 0);
    }

    #[test]
    fn can_push_back() {
        let mut list = DoublyLinkedList::new();
        assert_eq!(list.pop_back(), None);

        list.push_back(3);
        list.push_back(4);
        list.push_back(5);
        assert_eq!(list.pop_back(), Some(5));

        list.push_back(6);
        list.push_back(7);
        assert_eq!(list.pop_back(), Some(7));
        assert_eq!(list.pop_back(), Some(6));
        assert_eq!(list.pop_back(), Some(4));
        assert_eq!(list.pop_back(), Some(3));

        list.push_back(2);
        assert_eq!(list.pop_back(), Some(2));
        assert_eq!(list.pop_back(), None);
        assert_eq!(list.len(), 0);
    }

    #[test]
    fn it_drops_correctly() {
        let mut list = DoublyLinkedList::new();
        for i in 0..3 {
            list.push_back(i);
        }

        drop(list);
    }

    #[test]
    fn can_iterate_forward() {
        let mut list = DoublyLinkedList::new();
        for i in 0..10 {
            list.push_front(i);
        }

        assert!(Iterator::eq(list.into_iter(), (0..10).rev()));
    }

    #[test]
    fn can_iterate_back() {
        let mut list = DoublyLinkedList::new();
        for i in 0..10 {
            list.push_front(i);
        }

        assert!(Iterator::eq(list.into_iter().rev(), 0..10));
    }
}

Summary

This article discussed what Doubly Linked List is, when it’s used, and how it’s implemented. We also tested it properly and implemented comment traits such as Iterator and Drop.

You can view the final code in my public repo.

General Idea#

Representation#

ListNode Implementation#

Doubly Linked List Implementation#

Structure and basic methods#

Push methods#

Pop methods#

Drop Implementation#

Iterator Implementation#

Testing#

Summary#